























3 августа в нашей компании прошел ранее анонсированный мастер-класс «Управление производством на основании численных данных».
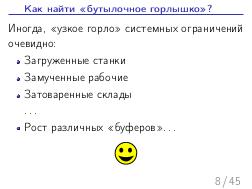
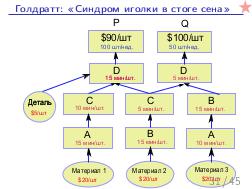
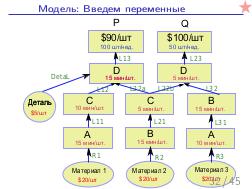
Возможно его название звучало несколько скучно, но на самом деле, тема основана на культовой бизнес-литературе — произведениях доктора Элии Голдратта, автора производственной Теории Ограничений, основной постулат которой заключался от отказе от бессмысленной и беспощадной борьбы за тотальную производительность, вместо чего он предлагал сконцентрироваться на определении узких мест в производстве и продаже, и борьбе с ними, не взирая на падение локальных показателей оптимальности. Забавный был и способ изложения этой теории — в виде серии бизнес-производственных-романов («Цель», «Цель-2», «Критическая цепь», и др.), где главный герой, стартуя из безнадежной ситуации (бизнес разоряется, увольняют из университета, жена ушла, денег нет, пиджак в пыли, под кроватью брюки…) сконцентрировавшись на ключевых проблемах, находил серию эффективных решений в духе теории ограничений, и выходил победителем из сложившихся ситуаций. В общем, несмотря на некоторую инфантильность сюжета и бизнес-ситуаций с точки зрения реальностей современного мира, мы обязательно рекомендуем всем прочитать эти книги (там только о решении проблем на производстве, но и о решении семейных проблем). А конкретно этот тренинг ведущий Сергей Мартыненко основал на книге «Синдром стога сена» (по ссылке перевод первой части), где на 40 страницах текста без малейшей романтики и лирики рассматривается в цифрах оптимизация некоторого модельного производства, и где «на пальцах» читателя убеждают, что для достижения максимальной прибыли нужно жертвовать локальными оптимумами, и принимать решения, часто интуитивно непонятные. Сергей также приводил пример, иллюстрирующий, что похожие сценарии, когда действия, вроде бы направленные на улучшение процесса, на самом деле приводят к возникновению «бутылочного горла», бывают не только в материальном производстве, но и в разработке софта.
Вот обработанное от шума видео, которое как обычно, можно просмотреть в броузере или скачать для обычного просмотра:
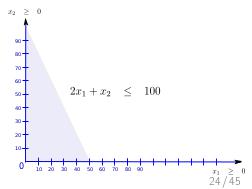
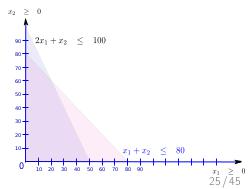
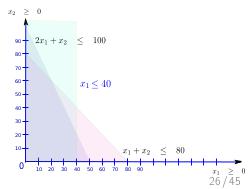
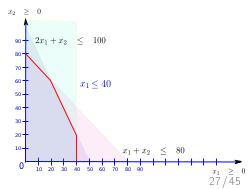
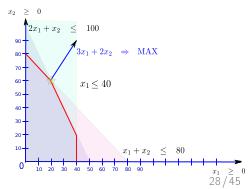
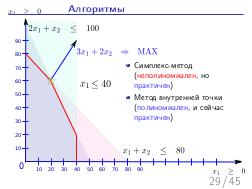
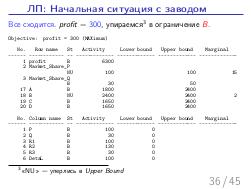
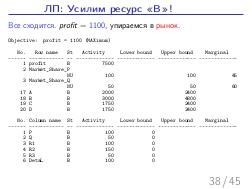
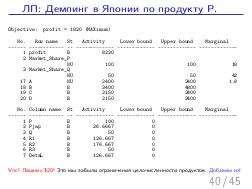
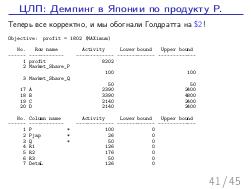
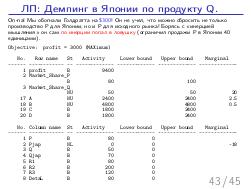
Далее, был доклад Стаса Фомина: «Теория ограничений и Линейное Программирование», о возможности математического моделирования широкого класса производственных задач, в контексте и на материале того же «Стога сена». Математическое моделирование — это мощный и гуманный инструмент поиска «бутылочного горлышка» на математической модели производства, позволяющий прогнозировать изменения и дрейф ограничений, без необходимости натурных экспериментов на живых людях и работающем производстве, как происходило в романах Голдратта. А линейное программирование — простая и в то же время мощная модель, в которой каждый менеджер должен уметь формулировать подходящие задачи оптимизации. На этом докладе сначала было сделано введение в постановку задач линейного программирования на совершенно классическом игрушечном примере, а затем, за двадцать минут были вживую, с участием зрителей, сформулированы и решены все вариации задач из «Синдрома стога сена», причем оказалось, что бездушный компьютер, снабженный формулировкой задачи, нашел более оптимальное решение, чем сам Голдратт в этой книге (это было обнаружено совершенно случайно, при подготовке презентации за час до выступления). Таким образом, были подведены итоги:
Опубликован видео-скринкаст, рекомендуем его смотреть в полноэкранном режиме. Впрочем можно скачать HD-видео, оно очень компактное, 80Mb.
Для очень быстрого поверхностного ознакомления опубликованы слайды презентации (но лучше смотрите видео):
Любые правки этой статьи будут перезаписаны при следующем сеансе репликации. Если у вас есть серьезное замечание по тексту статьи, запишите его в раздел «discussion».